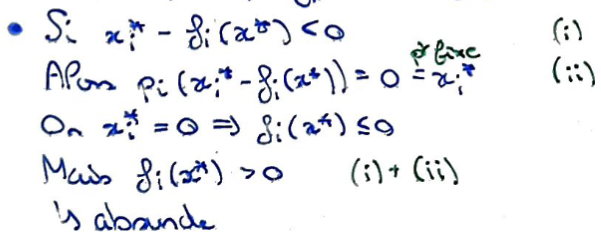Théorème de Poincaré-Miranda - Math'φsics

Théorème de Poincaré-Miranda

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Théorème de Poincaré-Miranda :
\(f_1,\dots,f_n:[0,1]^n\to{\Bbb R}\)

$$\forall i\in[\![1,n]\!],\qquad f_i(x)\leqslant0\text{ si }x_i=-1\quad\text{ et }\quad f_i(x)\geqslant0\text{ si }x_i=1$$

$$\Huge\iff$$

$$\exists x\in[0,1]^n,\quad f_1(x)=\dots=f_n(x)=0$$
Démonstration du théorème de Poincaré-Miranda :

Poser \(\varphi\) la différence entre \(x\) et \(f(x)\), où on restreint les résultats à \([0,1]\).

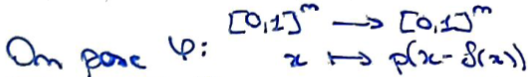
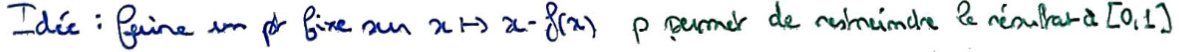
D'après le Théorème du point fixe de Brouwer, cette fonction admet un point fixe \(x^*\).

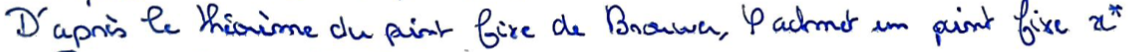
Si \(x^*-f_i(x^*)\in[0,1]\), alors par définition de \(\varphi\) et en utilisant le fait que \(x^*\) est point fixe, on a \(f_i(x^*)=0\).

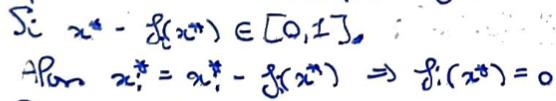
Le cas \(x_i^*-f_i(x^*)\lt 0\) est absurde car on aurait \(x_i^*=0\) par définition de \(\varphi\) et \(f_i(x^*)\gt 0\), ce qui contredit l'hypothèse.